Območje kroga: formula. Zakaj je ploščina kroga, opisanega in vpisanega v kvadrat, enaka pravokotnemu enakokrakemu trikotniku, pravokotnemu enakokrakemu trapezu?

Kako najti površino kroga? Najprej poiščite polmer. Naučite se reševati preproste in zapletene naloge.

Krog je zaprta krivulja. Vsaka točka na krožnici bo enako oddaljena od središča. Krog je ploščata oblika, zato je reševanje naloge iskanja območja preprosto. V tem članku bomo razmislili, kako najti območje kroga, vpisanega v trikotnik, trapez, kvadrat in opisano v bližini teh številk.

Ploščina kroga: formula z uporabo polmera, premera, dolžine kroga, primeri reševanja problemov

Iskanje površine kroga figura, morate vedeti, da je to polmer, premer in število π.

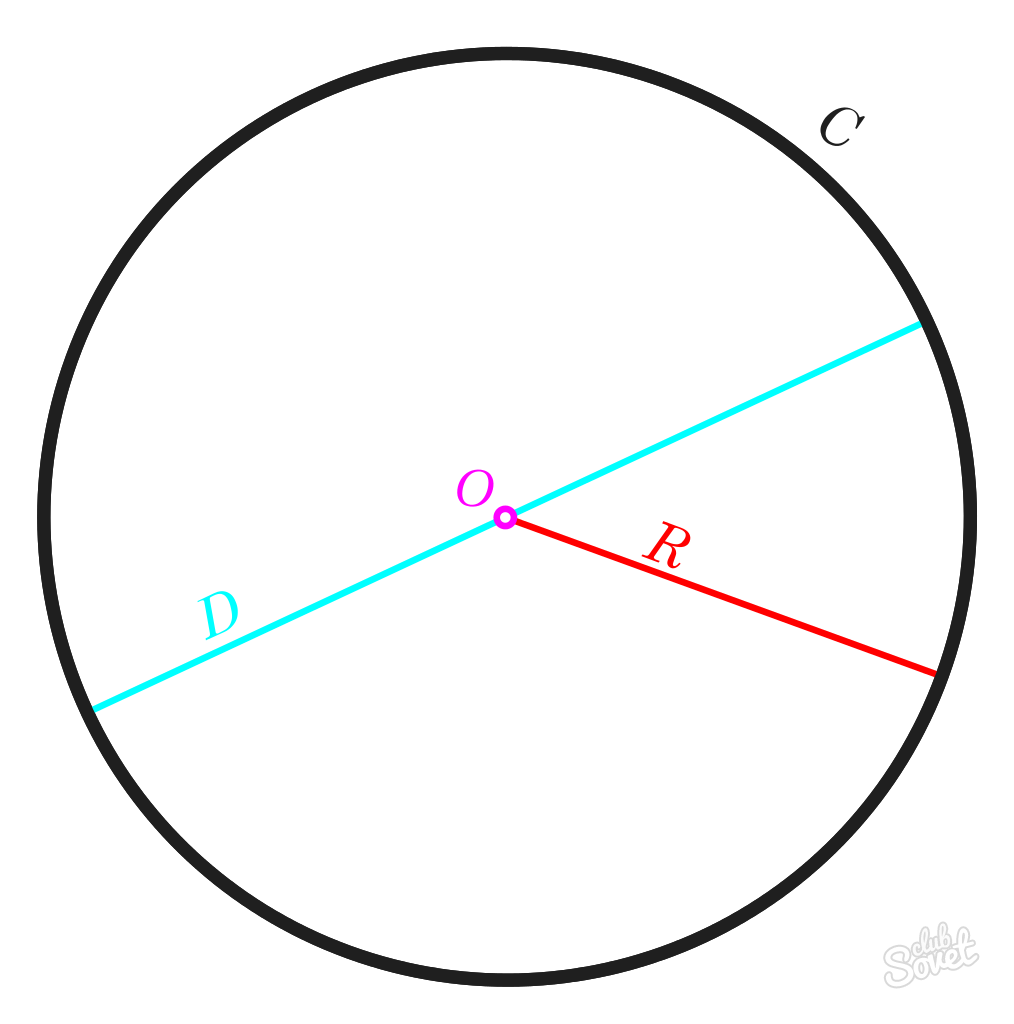
Polmer R je razdalja, ki jo omejuje središče kroga. Dolžine vseh R-polmerov enega kroga bodo enake.

Premer D je črta med katerima koli dvema točkama na krožnici, ki poteka skozi središčno točko. Dolžina tega segmenta je enaka dolžini polmera R, pomnoženega z 2.

Število π je konstantna vrednost, enaka 3,1415926. V matematiki se to število običajno zaokroži na 3,14.

Formula za iskanje površine kroga skozi polmer:

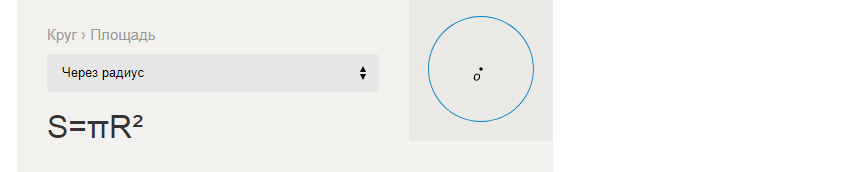
Primeri reševanja nalog za iskanje S-območja kroga skozi R-polmer:

---------- ---------------------------------- --

Naloga: Poiščite ploščino kroga, če je njegov polmer 7 cm.

Rešitev: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Odgovor: Ploščina kroga je 153,86 cm2.

Formula za iskanje S-območja kroga skozi D-premer:

Primeri reševanja nalog za iskanje S, če je D znan:

--------- --------------------------------

Naloga: Poiščite S kroga, če je njegov D enak 10 cm.

Rešitev: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Odgovor: Ploščina ravnega okroglega lika je 78,5 cm2.

Iskanje S kroga, če je znana dolžina kroga:

Najprej ugotovimo, koliko je polmer. Dolžina kroga se izračuna po formuli: L=2πR, zato bo polmer R enak L/2π. Zdaj najdemo površino kroga s formulo skozi R.

Razmislimo o rešitvi na primeru problema:

----------- -----------------------------

Naloga: Poiščite ploščino kroga, če je znana dolžina kroga L — 12 cm.

Rešitev: Najprej poiščemo polmer: R=L/2π=12/2*3,14=12/6,28=1,91.

Sedaj poiščemo površino skozi polmer: S=πR2=3,14*1,912=3,14*3,65=11,46 cm2.

Odgovor: Ploščina kroga je 11,46 cm2.

Površina kroga, vpisanega v kvadrat: formula, primeri reševanja problemov

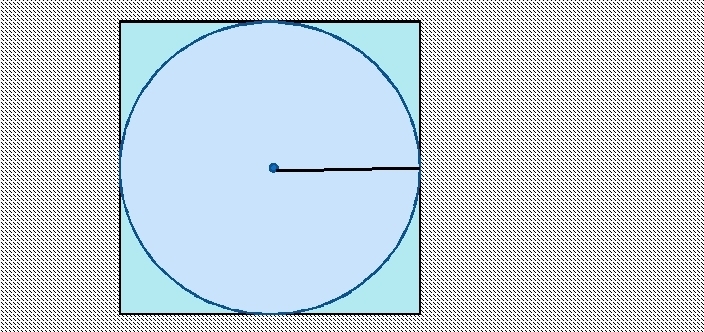
Iskanje ploščine kroga, včrtanega v kvadrat, je preprosto. Stranica kvadrata je premer kroga. Če želite najti polmer, morate stran deliti z 2.

Formula za iskanje površine kroga, vpisanega v kvadrat:

Primeri reševanja nalog za iskanje površine kroga, včrtanega v kvadrat:

-- ---------------------------------- ----

Naloga št. 1: Poznamo stranico kvadrata, ki je enaka 6 centimetrom. Poiščite S-območje včrtanega kroga.

Rešitev: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Odgovor: Ploščina ravnega okroglega lika je 28,26 cm2.

---------------------------------------------- -----------

Naloga #2 :Poiščite S kroga, včrtanega kvadratu, in njen polmer, če je ena stranica enaka a=4 glej

Rešite kot sledi : Najprej najdemo R=a/2=4/2=2 glej

Zdaj bomo našli ploščino kroga S=3,14*22=3,14*4=12,56 cm2.

Odgovor: Ploščina ravnega krožnega lika je 12,56 cm2.

Ploščina kroga, opisanega okoli kvadrata: formula, primeri reševanja problemov

Malo težje je najti ploščino okrogle figure, opisane okoli kvadrata. Toda če poznate formulo, lahko hitro izračunate to vrednost.

Formula za iskanje S kroga, opisanega okoli kvadrata:

Primeri reševanja nalog za iskanje ploščine kroga, opisanega okrog kvadrata:

Problem

Območje kroga, vpisanega v pravi in ​​enakokraki trikotnik: formula, primeri reševanja problemov

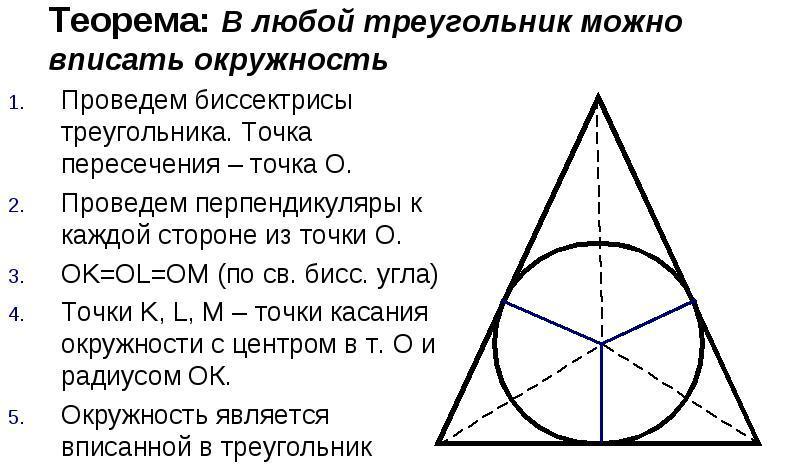
Krožnica, včrtana v trikotnik, je krožnica, ki se dotika vseh treh strani trikotnika. Vsakemu trikotniku lahko vpišemo krog, vendar samo enega. Središče kroga bo točka presečišča simetral kotov trikotnika.

Formula za iskanje površine kroga, vpisanega v enakokraki trikotnik:

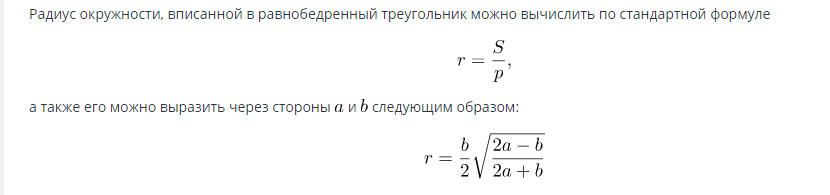
Ko je polmer znan, lahko ploščino izračunamo po formuli: S=πR2.

Formula za iskanje površine kroga, včrtanega v pravokotni trikotnik:

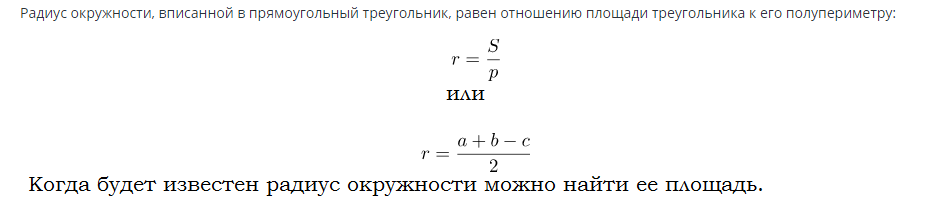
Primeri rešitev naloge:

Problem # 1

)

Če morate v tej nalogi najti tudi površino kroga s polmerom 4 cm, potem lahko to storite po formuli: S=πR2

Naloga št. 2

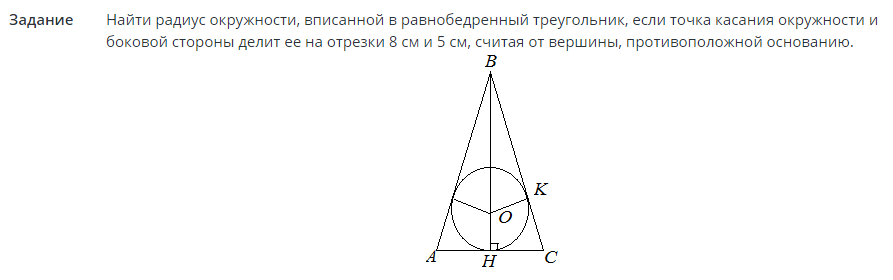
Rešitve:

Zdaj, ko je polmer znan, je mogoče površino kroga najti v smislu polmera. Glej formulo zgoraj v besedilu.

Naloga #3

Ploščina kroga, opisanega okoli pravokotnega in enakokrakega trikotnika: formula, primeri reševanja nalog

Vse formule za iskanje območja kroga se zmanjša na dejstvo, da morate najprej najti njegov polmer. Ko je radij znan, je iskanje območja preprosto, kot je opisano zgoraj.

​​​​

Ploščino kroga, opisanega okoli pravokotnega in enakokrakega trikotnika, dobimo z naslednjo formulo:

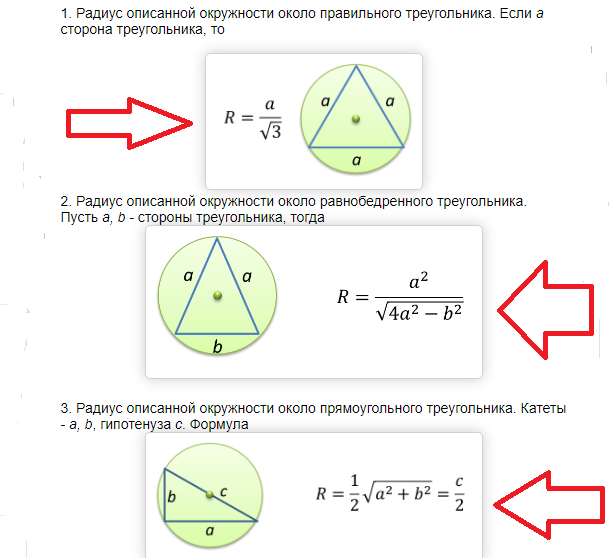
Primeri reševanja nalog:

Tukaj je še en primer reševanja problem pri uporabi Heronove formule.

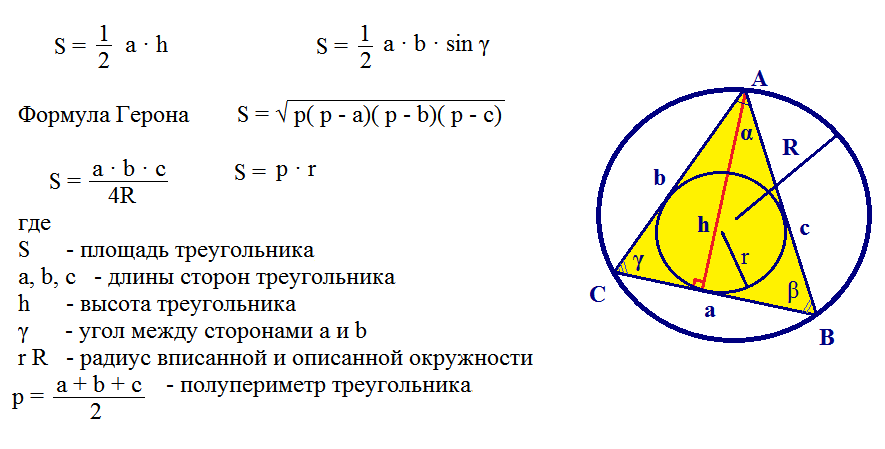
Težko je rešiti podobne težave, vendar jih je mogoče premagati, če poznate vse formule. Takšne naloge učenci rešujejo v 9. razredu.

Ploščina kroga, včrtanega v pravokotni in enakokraki trapez: formula, primeri reševanja problemov

Na primer, enakokrakemu trapezu je vpisana krog, ki je na stični točki, deli eno stran na segmenta m in n.

Za rešitev te težave morate uporabiti naslednje formule:

Iskanje površine kroga, vpisanega v pravokotni trapez, se izvede po naslednji formuli:

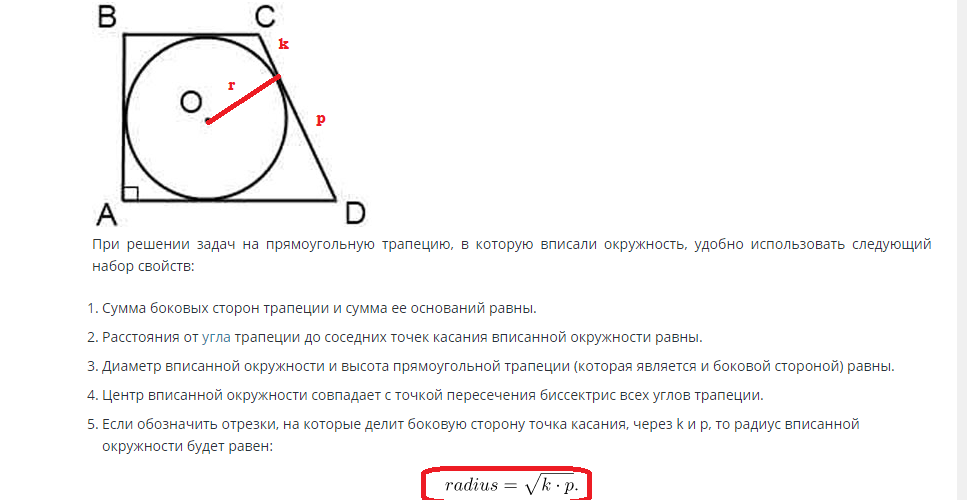
Če je stran znana, je polmer mogoče najti s to vrednostjo. Višina stranice trapeza je enaka premeru kroga, polmer pa polovica premera. V skladu s tem je polmer enak R=d/2.

Primeri reševanja nalog:

Ploščina kroga, opisanega okoli pravokotnega in enakokrakega trapeza: formula, primeri reševanja nalog

Trapezu je mogoče včrtati v krogu, ko je vsota nasprotnih kotov 180°. Zato lahko včrtamo le enakostranični trapez. Polmer za izračun površine kroga, opisanega v bližini pravokotnega ali enakokrakega trapeza, se izračuna po naslednjih formulah:

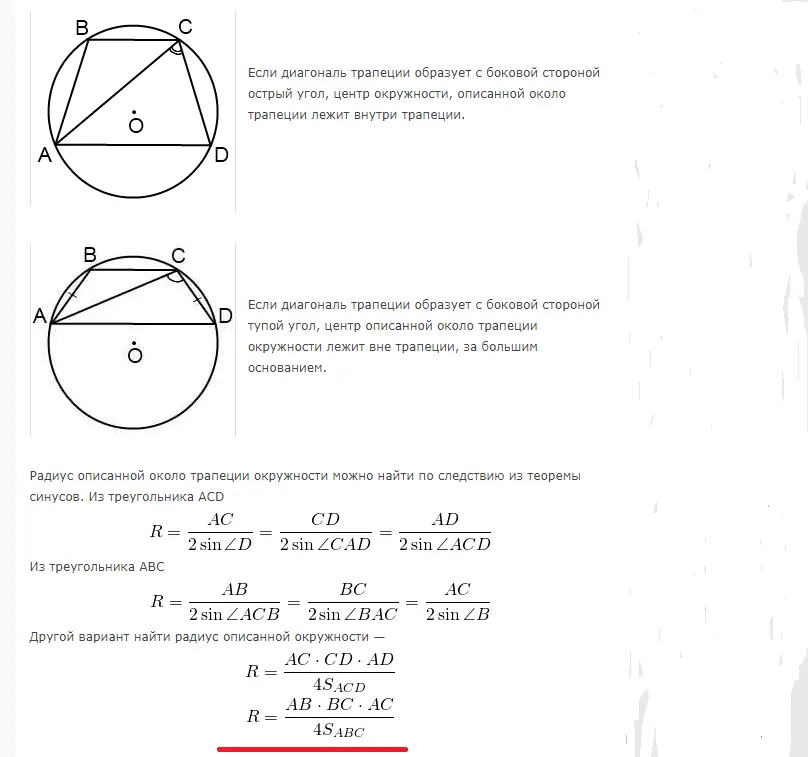
Primeri reševanja nalog:

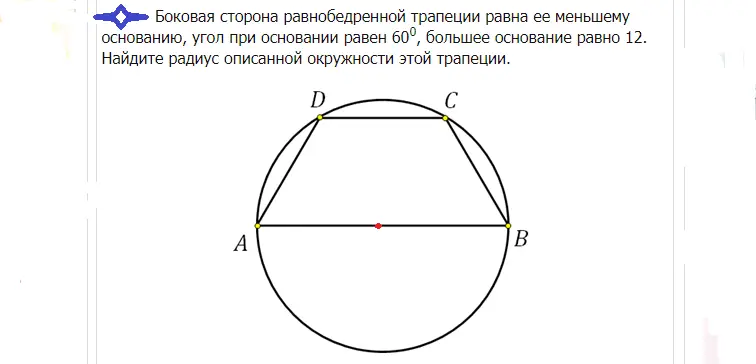
Rešitev: Velika osnova gre v tem primeru skozi središče, saj je v krog vpisan enakokraki trapez. Središče deli to osnovo točno na polovico. Če je osnova AB enaka 12, potem lahko polmer R najdete na naslednji način: R=12/2=6.

Odgovor: Polmer je 6.

V geometriji je pomembno poznati formule. Nemogoče pa si je zapomniti vse, zato je tudi na številnih izpitih dovoljeno uporabiti poseben obrazec. Vendar je pomembno, da znamo najti pravo formulo za rešitev te ali one težave. Vadite reševanje različnih problemov za iskanje polmera in površine kroga, da boste lahko pravilno nadomestili formule in dobili natančne odgovore.

Video: Matematika | Računanje ploščin kroga in njegovih delov