Formula za čas, hitrost in razdaljo: 4. razred. Kako najti čas, če poznaš hitrost in razdaljo? Kako najti hitrost, če sta znana čas in razdalja? Kako najti razdaljo, če sta znana čas in hitrost? Graf odvisnosti hitrosti telesa od časa

Kako rešiti gibalne naloge? Formula za razmerje med hitrostjo, časom in razdaljo. Naloge in rešitve.

Formula za odvisnost časa, hitrosti in razdalje za 4. razred: kako so označeni hitrost, čas, razdalja?

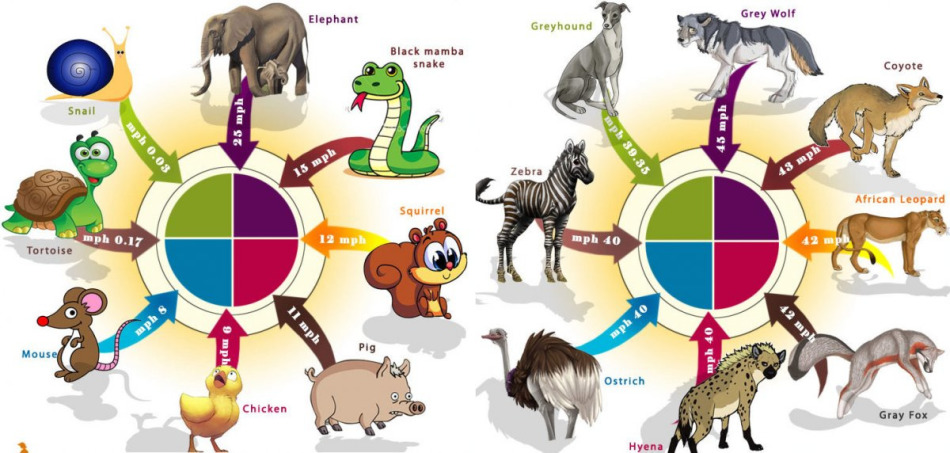
Ljudje, živali ali stroji se lahko premikajo z določeno hitrostjo. Lahko gredo določeno pot v določenem času. Na primer: danes lahko prideš v šolo v pol ure. Hodite z določeno hitrostjo in v 30 minutah prehodite 1000 metrov. V matematiki pot, ki jo premagamo, označujemo s črkoS. Hitrost označujemo s črko v. In čas, za katerega je pot opravljena, je označen s črko t.

• Pot —S
• Hitrost — v
• Čas —t

Če zamujate v šolo, lahko isto pot opravi v 20 minutah, s čimer povečate svojo hitrost. To pomeni, da lahko isto pot prehodimo v različnih časih in z različnimi hitrostmi.

Kako je čas potovanja odvisen od hitrosti?

Višja kot je hitrost, hitreje bo prevožena razdalja. In manjša kot je hitrost, dlje bo trajalo potovanje.

​​​​

Kako najti čas ob poznavanju hitrosti in razdalje?

Da bi našli čas, ki je bil potreben za prevoženo razdaljo, morate poznati razdaljo in hitrost. Če razdaljo delite s hitrostjo, boste izvedeli čas. Primer takšne naloge:

Naloga o zajcu. Zajec je bežal pred volkom s hitrostjo 1 kilometer na minuto. Do svoje luknje je pretekel 3 kilometre. Čez nekaj časa je Hare pobegnil v luknjo?

Kako enostavno je rešiti težave z gibanjem, kjer morate najti razdaljo, čas ali hitrost?

1. Pozorno preberi nalogo in ugotovi, kaj je znano iz pogoja težave.
2. Zapišite te podatke na osnutek.
3. Napišite tudi, kaj je neznano in kaj je treba najti
4. Uporabite formulo za naloge razdalje, časa in hitrosti
5. Vnesite znane podatke v formuli in reši nalogo

Rešitev naloge o zajcu in volku.

• Iz pogoja naloge ugotovimo, da poznamo hitrost in razdaljo.
• Iz pogoja naloge ugotovimo tudi, da moramo najti čas, v katerem je zajec pritekel do luknje.

Te podatke zapišemo na primer v osnutek:

Razdalja do luknje — 3 kilometre

Hitrost zajca — 1 kilometer v 1 minuti

Čas ni znan

Zdaj zapišimo isto z matematičnimi simboli:

J— 3 kilometre

V — 1 km/min

t—?

Prikličemo in zapišemo formulo za iskanje časa v zvezek:

t = S: v

Zdaj zapišemo rešitev naloge v številkah:

t = 3: 1 = 3 minute

Kako najti hitrost, če sta znana čas in razdalja?

Da bi našli hitrost, če sta znana čas in razdalja, je treba razdaljo deliti s časom. Primer takšne naloge:

Zajec je pobegnil od volka in tekel 3 kilometre do svoje luknje. To razdaljo je premagal v 3 minutah. Kako hitro je tekel zajec?

Rešitev gibalne naloge:

1. V osnutku pišemo, da poznamo razdaljo in čas.
2. Iz pogoja naloge ugotovimo, da moramo najti hitrost
3. Spomnimo se formule za iskanje hitrosti.

Formule za reševanje takih problemov so prikazane na spodnji sliki.

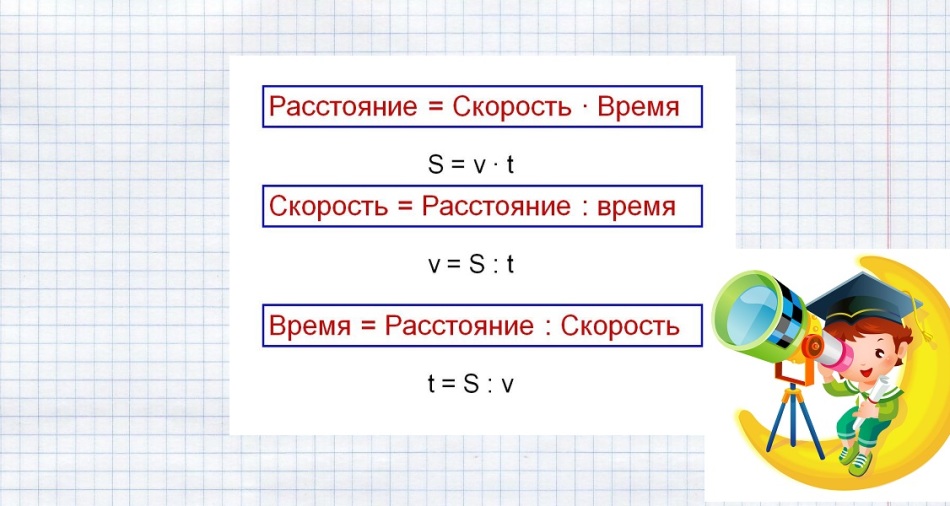
Nadomestite znane podatke in rešite nalogo:

Razdalja do luknje je 3 kilometre

Čas, ki ga je zajec potreboval, da je dosegel luknjo, je bil 3 minute

Hitrost ni znana

Zapišimo te znane podatke v matematičnih simbolih

S— 3 kilometri

 t— 3 minute

v —?

Zapišemo formulo za iskanje hitrosti

v = S: t

Sedaj zapišimo rešitev naloge v številkah:

v = 3: 3 = 1 km/min

Kako najti razdaljo, če čas in hitrost sta znana?

Če želite najti razdaljo, če sta znana čas in hitrost, pomnožite s hitrostjo. Primer takšne naloge:

Zajec je volku bežal s hitrostjo 1 kilometer v 1 minuti. Potreboval je tri minute, da je tekel do luknje. Kako daleč je tekel zajec?

Rešitev naloge: V osnutek zapišemo, kaj vemo iz pogoja naloge:

Hitrost zajca je 1 kilometer. v 1 minuti

Čas, ko je zajec tekel do luknje - 3 minute

Razdalja - neznana

Zdaj pa zapišimo isto z matematičnimi simboli:

v — 1 km/min

t— 3 minute

S —?

Spomnimo se formule za iskanje razdalje:

S = v ⋅ t

Zdaj zapišemo rešitev naloge v številkah:

S = 3 ⋅ 1 = 3 km

Kako se naučiti reševati zahtevnejše naloge?

Da bi se naučili reševati bolj zapletene naloge, morate razumeti, kako reševati preproste, zapomniti si, kateri znaki označujejo razdaljo, hitrost in čas. Če se matematičnih formul ne morete spomniti, jih zapišite na list papirja in imejte pri reševanju nalog vedno pri roki. Z otrokom rešujte preproste naloge, ki si jih lahko izmislite na poti, na primer med sprehodom.

Merske enote

​​

Pri reševanju nalog o hitrosti, času in razdalji se pogosto zmotijo, ker pozabijo pretvoriti merske enote.

POMEMBNO: Merske enote so lahko poljubne, če pa so v isti nalogi različne merske enote, jih pretvorite v iste. Na primer, če se hitrost meri v kilometrih na minuto, mora biti razdalja predstavljena v kilometrih, čas pa v minutah.

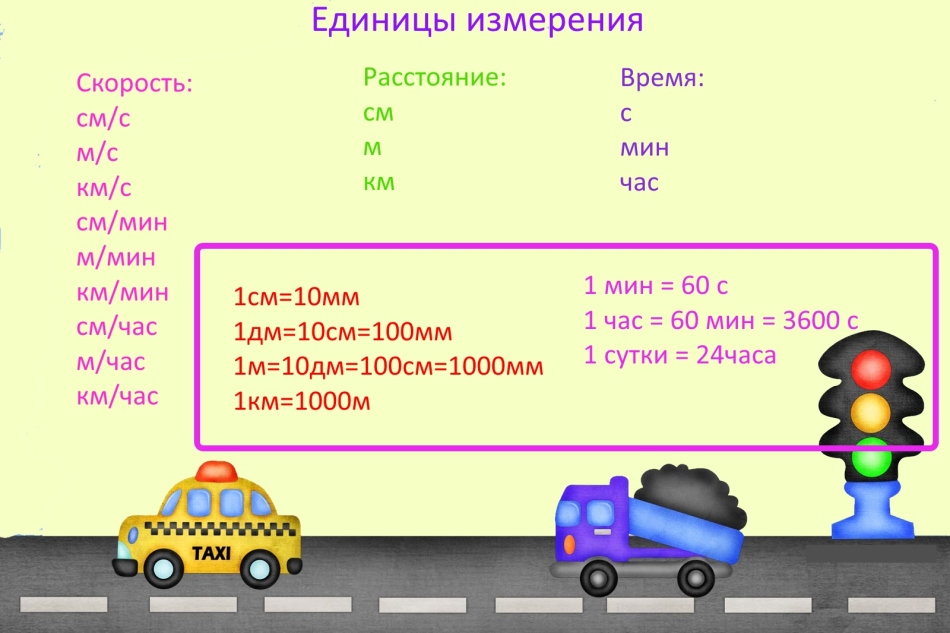
Za radovedne : Splošno sprejet sistem mer se imenuje metrika, vendar ni bilo vedno tako in v stari Rusiji so uporabljali druge merske enote.

Problem Boa : Slonji mladič in opica sta izmerila dolžino boa v ​​korakih. Pomikala sta se drug proti drugemu. Hitrost opice je bila 60 cm v eni sekundi, hitrost slonjega mladiča pa 20 cm v eni sekundi. Za merjenje so porabili 5 sekund. Kakšna je dolžina boe? (rešitev pod sliko)

<> Rešitev:

Iz pogoja naloge ugotovimo, da poznamo hitrost opice in slonjega mladiča ter čas, ki sta ga potrebovala, da izmerita dolžino udava.

Zapišimo te podatke:

Hitrost opice je 60 cm/s

Hitrost slonjega mladiča je 20 cm/s

Čas — 5 sekund

Razdalja neznana

Te podatke zapišimo z matematičnimi simboli:

v1 — 60 cm/s

v2 — 20 cm/s

t — 5 sekund

S —?

Zapišimo formulo za razdaljo, če sta znana hitrost in čas:

S = v ⋅ t

Preštejmo razdaljo, ki jo je prepotovala opica:

S1 = 60 ⋅ 5 = 300 cm

Zdaj pa preštejmo, koliko je slonček prehodil:

S2 = 20 ⋅ 5 = 100 cm

Seštejemo razdaljo, ki jo je prepotovala opica, in razdaljo, ki jo je prepotoval slonček:

S = S1 + S2 = 300 + 100 = 400 cm

Graf odvisnosti hitrosti telesa od časa: fotografija

Razdalja pokrito z različnimi hitrostmi je pokrito v različnih časih. Večja kot je hitrost, manj časa je potrebno za premikanje.

Tabela 4 razred: hitrost, čas, razdalja

Št.	Hitrost (km/h)	Čas (ura)	Razdalja (km)
1	5	2	?
2	12	?	12
3	60	4	?
4	?	3	300
5	220	?	440

Lahko fantazirate in pripravite naloge za mizo sami. Spodaj so naše možnosti za pogoje nalog:

1. Mama je poslala Rdečo kapico k babici. Deklica je bila ves čas motena in je skozi gozd hodila počasi, s hitrostjo 5 km/h. Za pot je porabila 2 uri. Koliko je v tem času prehodila Rdeča kapica?
2. Poštar Pečkin je na kolesu nosil paket s hitrostjo 12 km/h. Ve, da je razdalja med njegovo hišo in hišo strica Fedorja 12 km. Pomagaj Pečkinu izračunati, koliko časa bo trajalo potovanje?
3. Papa Ksyusha je kupil avto in se odločil, da bo družino odpeljal na morje. Avto je vozil s hitrostjo 60 km/h in na cesti je preživel 4 ure. Kakšna je razdalja med Ksyushino hišo in morsko obalo?
4. Race so se zbrale v klin in odletele v tople kraje. Ptice so 3 ure neumorno mahale s krili in v tem času prevozile 300 km. Kakšna je bila hitrost ptic?
5. Letalo AN-2 leti s hitrostjo 220 km/h. Vzletel je iz Moskve in leti v Nižni Novgorod, razdalja med tema mestoma je 440 km. Kako dolgo bo letalo na poti?

Odgovore na dane naloge najdete v spodnji tabeli:

)

Št.	Hitrost (km/h))	Čas (ura)	Razdalja (km)
1	5	2	10
2	12	1	12
3	60	4	240
4	100	3	300
5	220	2	440

Primeri reševanja nalog hitrosti, časa, razdalje za 4. razred

Če je v eni nalogi več premikajočih se predmetov, morate otroka naučiti, da gibanje teh predmetov obravnava ločeno in šele nato skupaj. Primer takšne naloge:

Dva prijatelja Vadyk in Tema sta se odločila, da gresta na sprehod in sta zapustila svoje hiše, da bi se srečala. Vadyk je vozil kolo, Tema pa je hodila. Vadyk je vozil s hitrostjo 10 km/h, Tema pa je hodila s hitrostjo 5 km/h. Uro kasneje sta se srečala. Kakšna je razdalja med hišama Vadyk in Tema?

Ta problem lahko rešimo s formulo za odvisnost razdalje od hitrosti in časa.

S = v ⋅ t

Razdalja, ki jo Vadyk prevozi s kolesom, bo enaka njegovi hitrosti, pomnoženi po času v tranzitu.

S = 10 ⋅ 1 = 10 kilometrov

Razdalja, ki jo subjekt prepotuje, se izračuna podobno:

S = v ⋅ t

Nadomestite digitalne vrednosti njegove hitrosti in časa v formulo

S = 5 ⋅ 1 = 5 kilometrov

Razdalji, ki jo je prepotoval Vadyk, je treba prišteti razdalji, ki jo je prepotoval Tema.

10 + 5 = 15 kilometrov

Kako se naučiti reševati zapletene probleme, ki zahtevajo logično razmišljanje?

Za razvoj otrokovega logičnega mišljenja je treba iz njih reševati preproste, nato zapletene logične naloge. Te naloge so lahko sestavljene iz več faz. Iz ene stopnje v drugo se lahko premaknete le, če je prejšnja rešena. Primer takšne naloge:

Anton je vozil kolo s hitrostjo 12 km/h, Lisa pa je vozila skiro s 2-krat manjšo hitrostjo od Antona, Denis pa hodil s hitrostjo 2-krat manjšo od Lizine. Kakšna je Denisova hitrost?

Za rešitev tega problema morate najprej poznati Lizino hitrost in šele nato Denisovo hitrost.

Dva kolesarja sta se odpravila iz različnih mest drug drugemu naproti. Enemu se je mudilo in je tekel s hitrostjo 12 km/h, drugi pa je vozil ležerno s hitrostjo 8 km/h. Razdalja med mesti, iz katerih so kolesarji odšli, je 60 km. Kako daleč bo prevozil vsak kolesar, preden se srečata? (rešitev pod sliko)

Rešitev:

• 12+8 = 20 (km/h) je skupna hitrost obeh kolesarjev oziroma hitrost, s katero sta se približevala drug drugemu
• 60: 20 = 3 (h) je čas, po katerem sta se kolesarja srečala
• 3 ⋅ 8 = 24 (km) je razdalja, ki jo prevozi prvi kolesar
• 12 ⋅ 3 = 36 (km) je pot, ki jo je prevozil drugi kolesar
• Preverite: 36+24=60 (km) je pot, ki jo prevozita kolesarja.
• Odgovor: 24 km, 36 km.

Otrokom ponudite, da v obliki igre rešijo naslednje naloge. Morda bodo želeli sami narediti problem glede prijateljev, živali ali ptic.

VIDEO: Gibalne težave